One of the more interesting revelations discovered during the 2014 Sony Pictures Entertainment hack was that actresses Jennifer Lawrence and Amy Adams made less money than their male costars for the movie American Hustle. Specifically, Lawrence and Adams earned 7% of the profits while their male co-stars earned 9%: a 28% increase in pay.
That made me curious: is the discrepancy in pay between male-leads and female-leads justifiable? Do movies with male lead actors generate more box office revenue than movies with female leads? Are movies with male leads better than those with female leads?
Using movie data from OMDb API, which is sourced from IMDb and Rotten Tomatoes data, I found that on average, blockbuster movies with male leads generate 22% more domestic box office revenue than those with female leads, and that this difference is statistically significant.
Setting Up the Movie Data

I’ve talked about processing the OMDb dataset in my previous post. For this analysis, I’ll be filtering on a specific subset of movies:
- Movies with at least $10 million in inflation-adjusted domestic box office revenue. My first analysis showed that there is a distinct cluster of movies above the $10M threshold specifically. These blockbusters are also what the public knows and best reflects the perception of the industry.
- Movies which were released in 2000 or later. There was missing box office revenue data I had found with earlier years so I would prefer to use more robust data to be safe. Additionally, this avoids the complicated issue of 20th-century gender politics in cinema, which I cannot easily address statistically.
After applying the filters and cleaning the data further to eliminate miscoded movies, I have created a dataset of 2,020 movies. No movies were removed as outliers in box office revenue (such as Star Wars VII and Avatar) since several tests failed to identify them as statistical outliers.
I identified the lead actor of each movie, using the first credited actor on the IMDb cast overview (NB: this may lead to counterintuitive behavior in casts with unknown leads; the first credited actor for Star Wars: The Force Awakens on IMDb is Harrison Ford, who is not the lead and I corrected it to Daisy Ridley in the data). Then I determined their gender by referencing a few gender/first-name mappings (with thanks to Matt Daniels and his great work on gender and film dialogue).
In all, the dataset has 467 (23%) of movies with a female lead actor, and 1,553 (77%) movies with a male lead actor. Both counts are more than enough for this analysis.
You can view and download the final dataset in this Google Sheet.
Distribution of Box Office Revenue
Let’s start with simple histograms of the box office data. What are the distributions of the data for each gender?
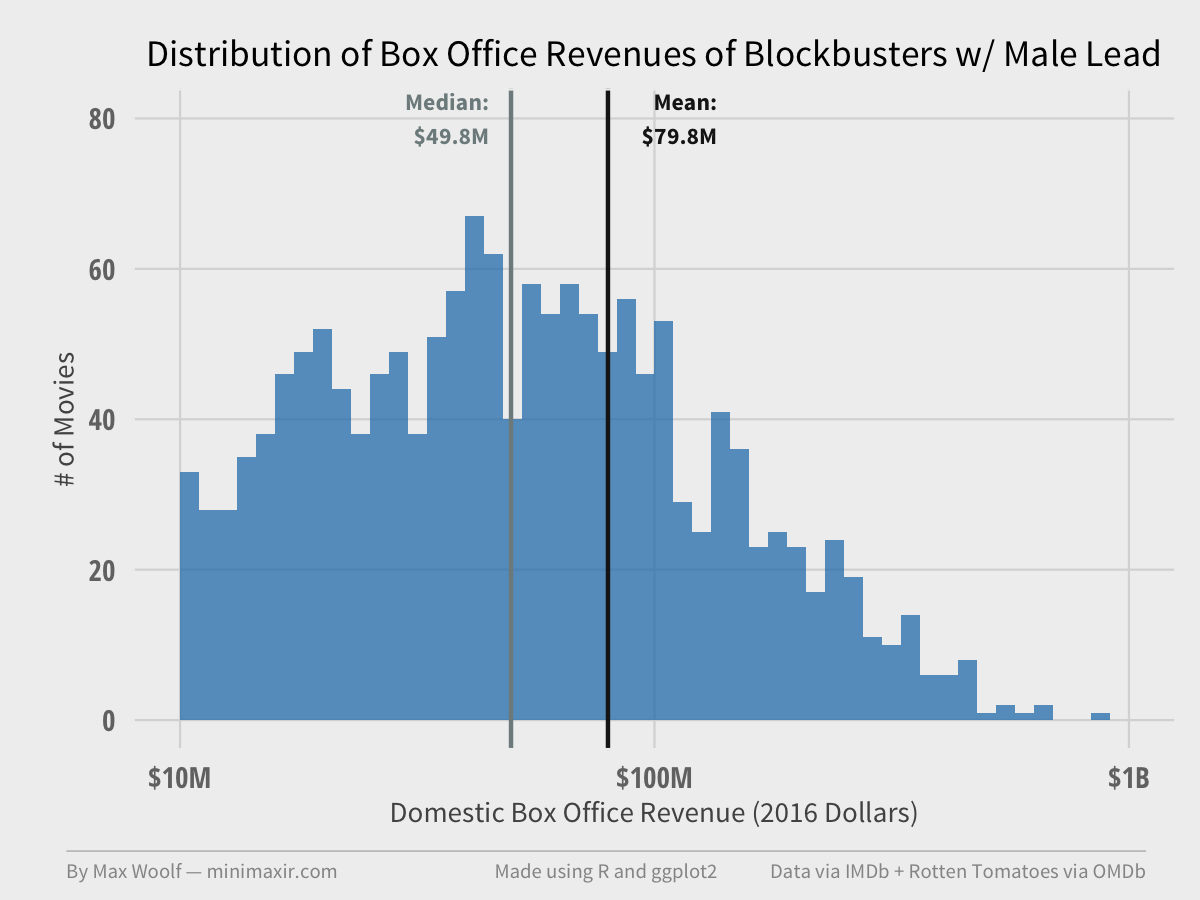
On average, blockbuster movies with male lead actors generate $79.8M in revenue. The distribution, even when log-scaled, is skewed right, with the median being much lower at $49.8M.
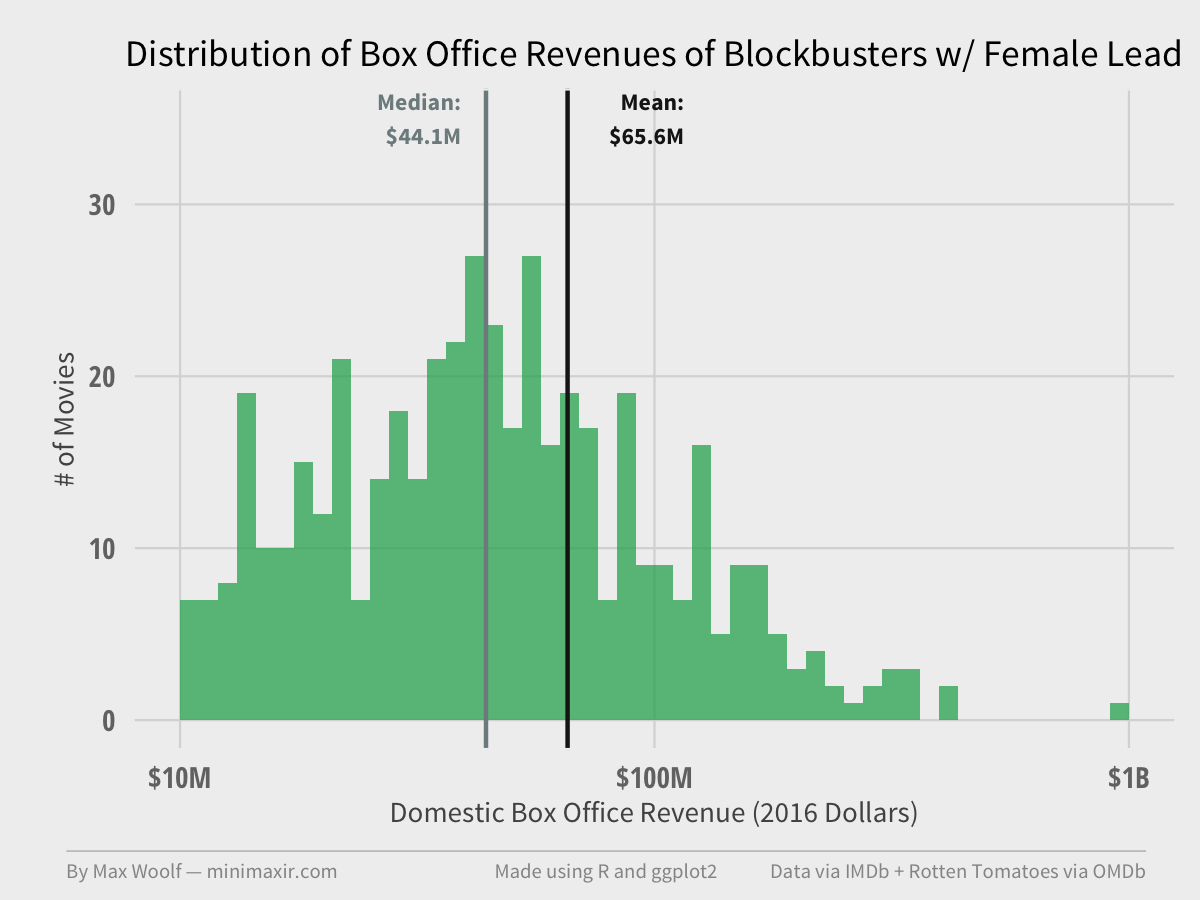
On average, blockbuster movies with female lead actors generate $65.6M in revenue. The general shape of the distribution is the same as with male lead actors.
Double-checking the math:
79.8M / 65.6M = 22% increase in average box office revenue for male-lead movies
So it is.
Let’s overlay the two distributions after normalizing and smoothing with a 2D kernel destiny estimator.
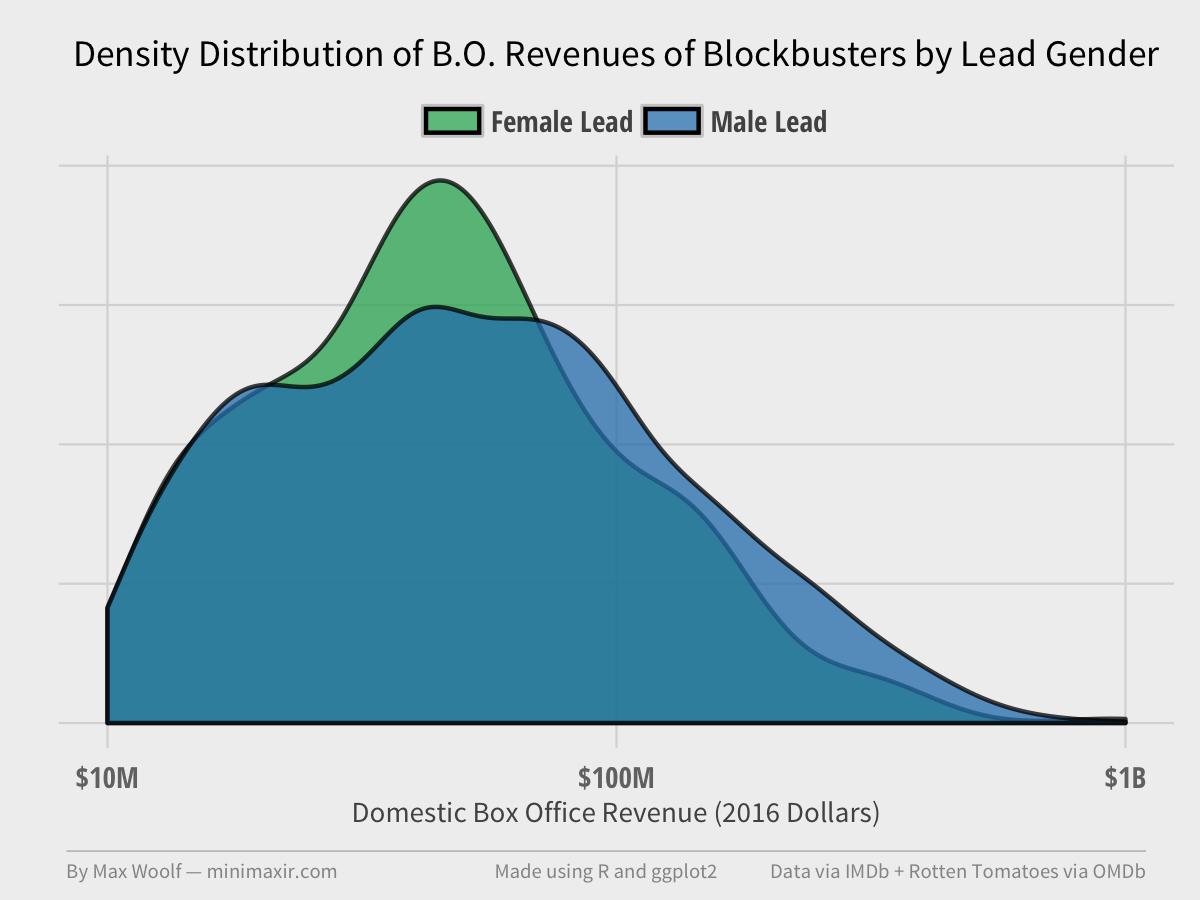
Female movies have a clear mode near its average, but male movies have a flatter distribution, with significantly more movies making 9 figures.
But is the difference between the two averages statistically significant? We can run two statistical tests between the box-office revenues of male-led and female-lead movies:
- The Kolmogorov–Smirnov test for determining if two populations have the same distribution. The null hypothesis is that the two are drawn from the same distribution; the alternative hypothesis is that the distributions are different. We reject the null hypothesis at the 95% level in favor of the alternative if the p-value of the test is less than 0.05. Running the test, p < 0.01, so we can say the distributions are statistically different. (the p-values are the same whether the box office revenues are log-transformed or not)
- The Wilcoxon rank-sum test for determining if the means (averages) of two populations are the same (null hypothesis) or different (alternative hypothesis). This test is used instead of a t-test if the populations are not Normally distributed, which is the case here. Running the test (one-sided, since only checking if a mean is greater), p < 0.01, so we can say the two means are statistically different. (again, the p-values are the same whether the box office revenues are log-transformed or not)
So we have statistical evidence that male-lead movies generate more money on average than female-led movies. But this claim is very serious, and as a result, we need even more proof.
The Resampling
Although 2,020 movies is a fair sample size by statistical standards, some may argue that the movies were chosen too arbitrarily and that there is not enough data to support the conclusions I make above. Enter bootstrap resampling, in which we resample the data randomly (with replacement) to generate pseudo-datasets, and then calculate aggregate statistics (e.g. the average) on that simulated dataset. Repeat a large number of times, and we can form confidence intervals for the true average of a given data set.
In this case, we resample the box office revenues, calculate the average box office revenue for both male-led and female-led movies, store the result away and resample the data again, and keep repeating until satisfied.
Here’s an animation of the resampling of both averages as the number of trials increases. As you can see, the shape of both distributions stabilize very quickly:
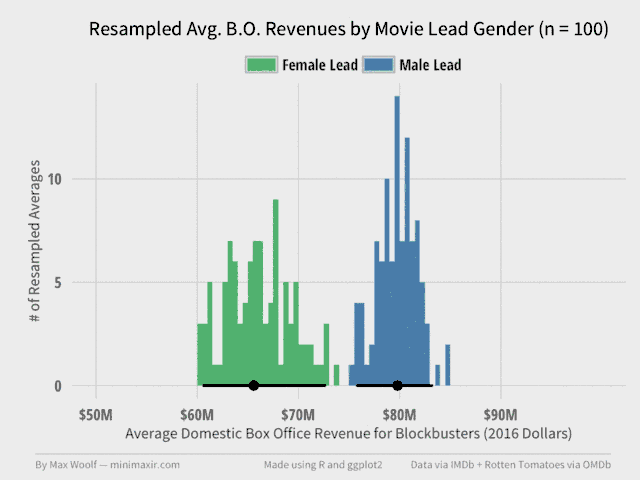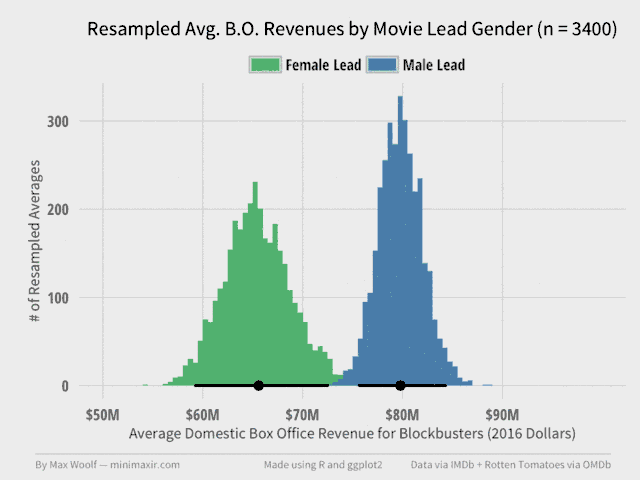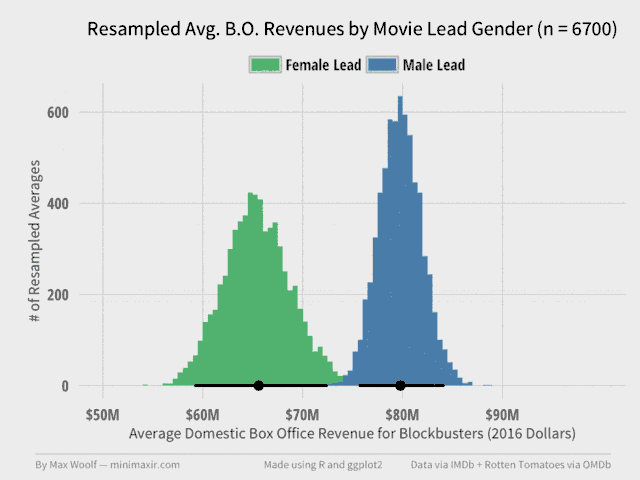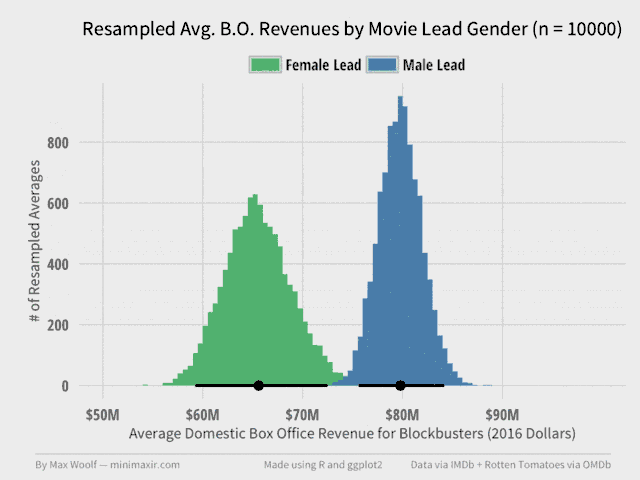
And the final plot, at 10,000 repetitions:
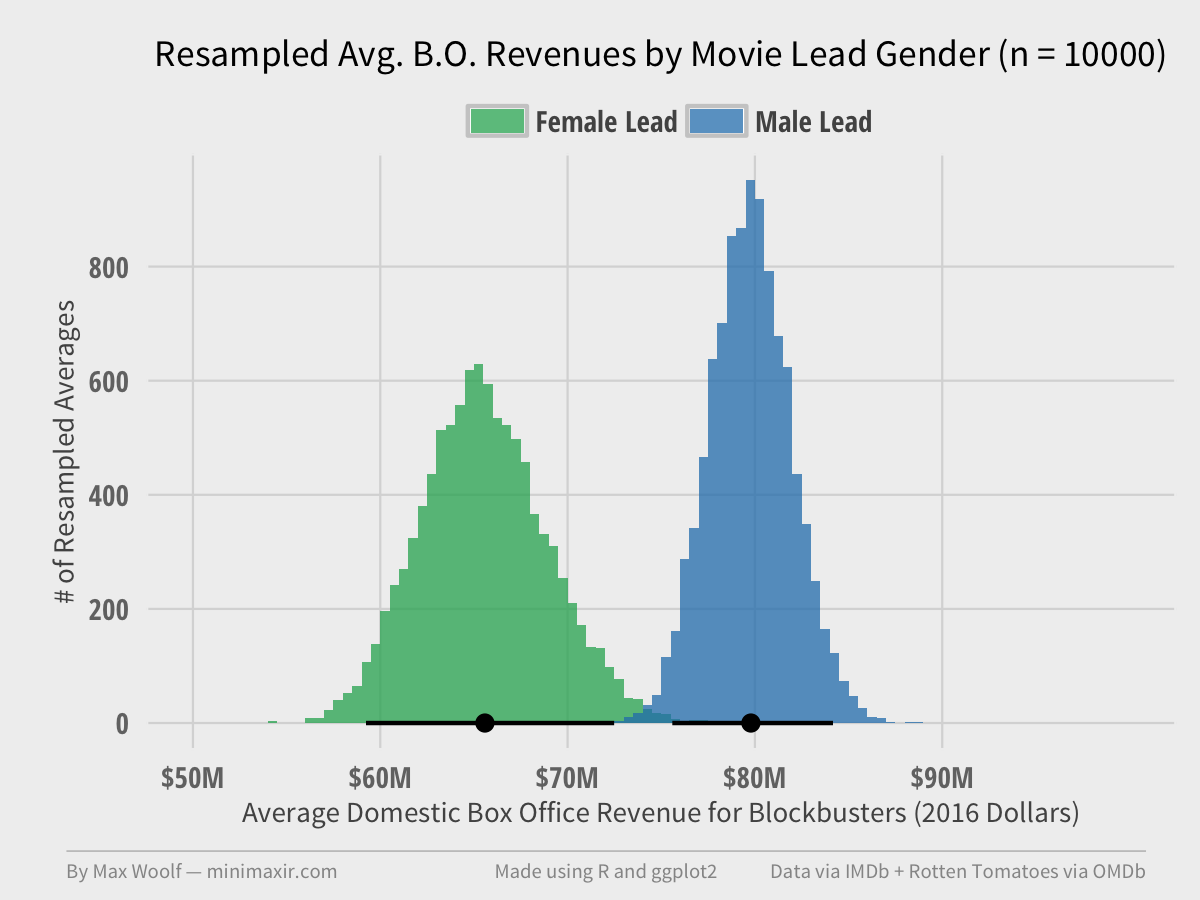
The dot on the bottom of each distribution represents the actual sample average value calculated during the analysis earlier, while the line range represents a 95% confidence interval for the true average revenue value for each gender. The distribution of male-led movie averages is more narrow than female-led movies because there are 3 times as many male-led movies in the dataset.
As you can see, the line ranges never intersect. Even in the most favorable scenario at the 95% confidence level, the average domestic box office revenue for male-led movies will be greater. Specifically, of the 10,000 trials, only 2 trials had the case where female-led movies had equal or greater average revenue than the corresponding male-led movie revenue average from the same resampling; this implies p < 0.01 for the statistical test on whether the means are same or different.
Interestingly, there’s a little overlap between in the distributions, which occurs when there are multiple instances of Star Wars VII in the resampled dataset and its high box office revenue pushes the entire female-lead average up very significantly.
Gender and Quality
It is also worth checking if male-led movies are better in quality than female-lead movies, as if that’s the case, it might provide a more logical explanation why male-led movies make more money.
Let’s check out the distribution of Rotten Tomatoes Tomatometer scores of blockbuster movies.
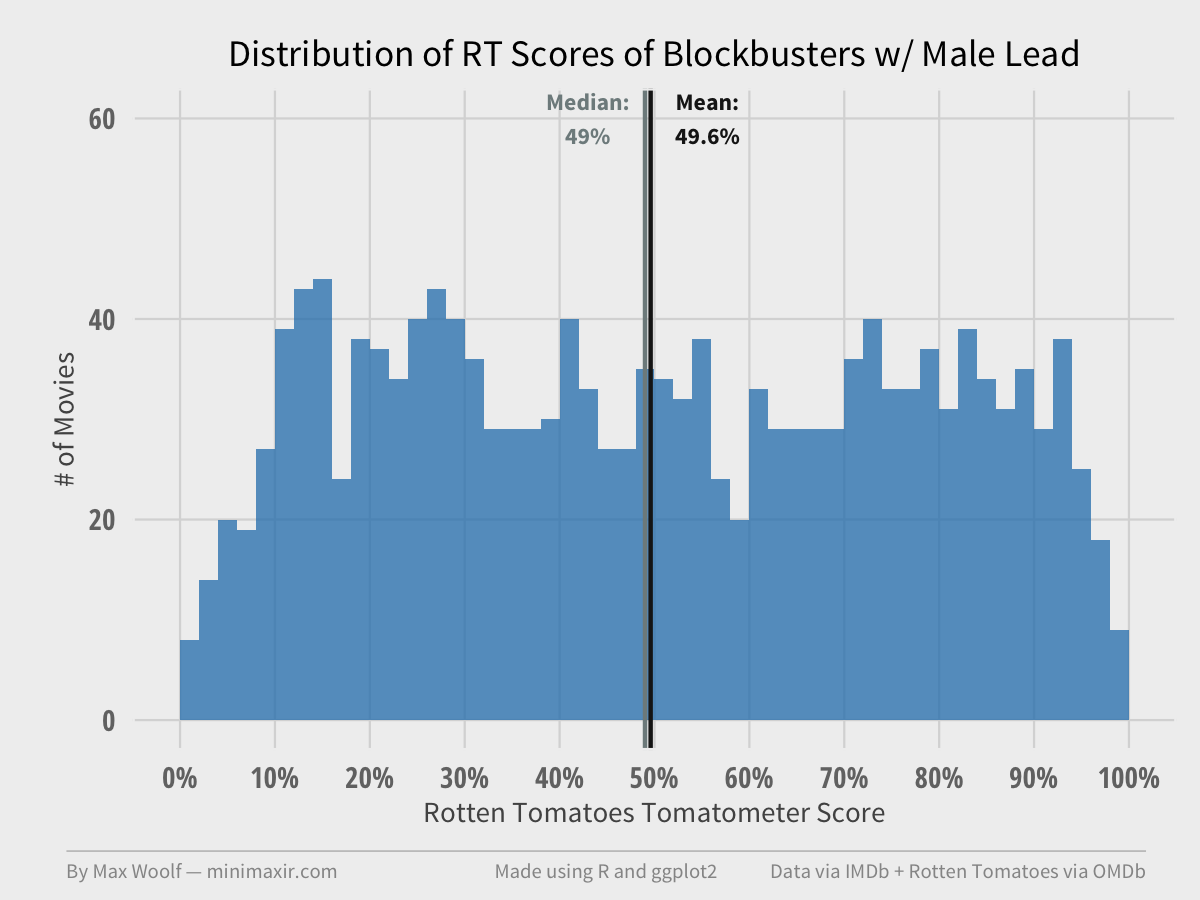
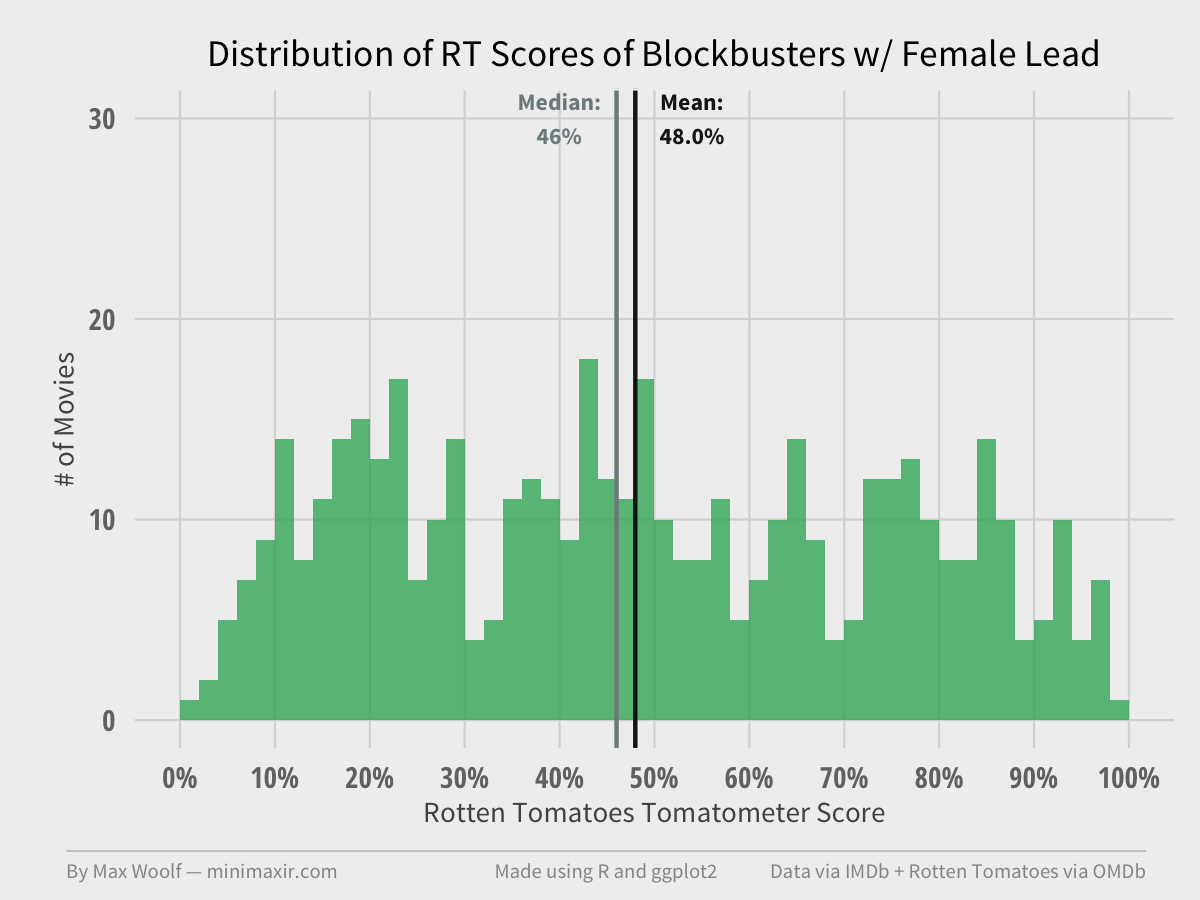
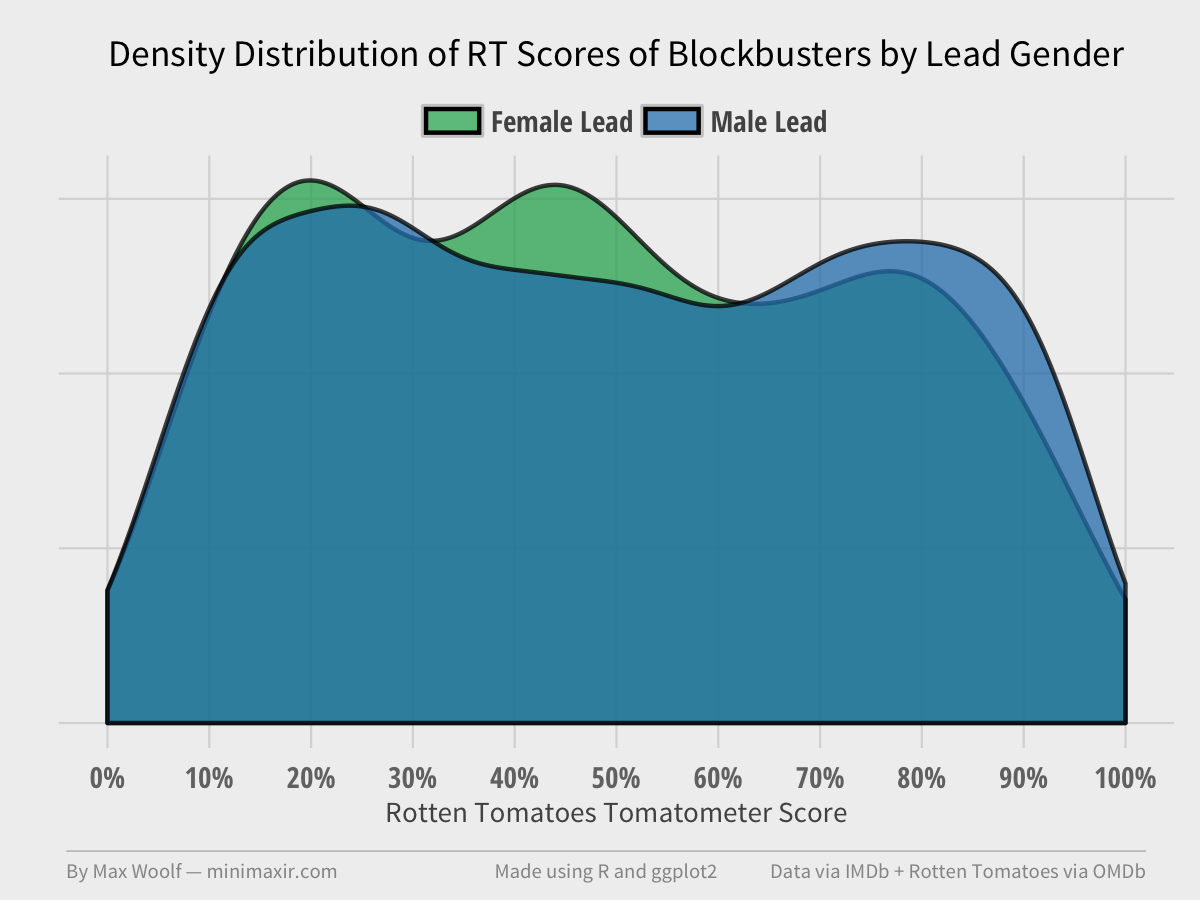
There’s no obvious difference. Female-led movies are about 2% points lower on average, but the general distribution is the same (uniform). Overlaying the two distributions shows as such.
The difference in averages is not statistically significant, as both the Kolmogorov–Smirnov test and the Wilcoxon rank-sum test fail to reject the null hypothesis at the 95% level (p = 0.37 and p = 0.13 respectively).
How about Metacritic scores?
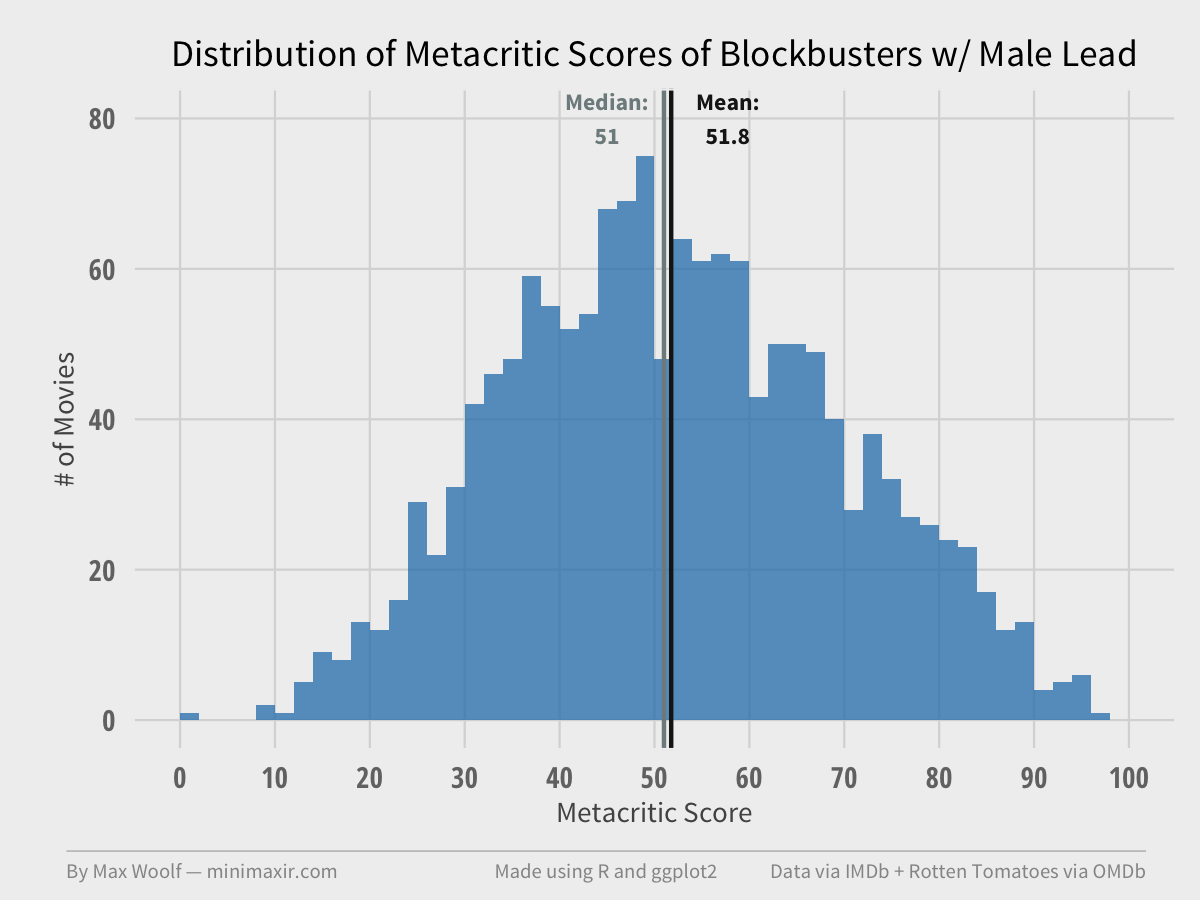
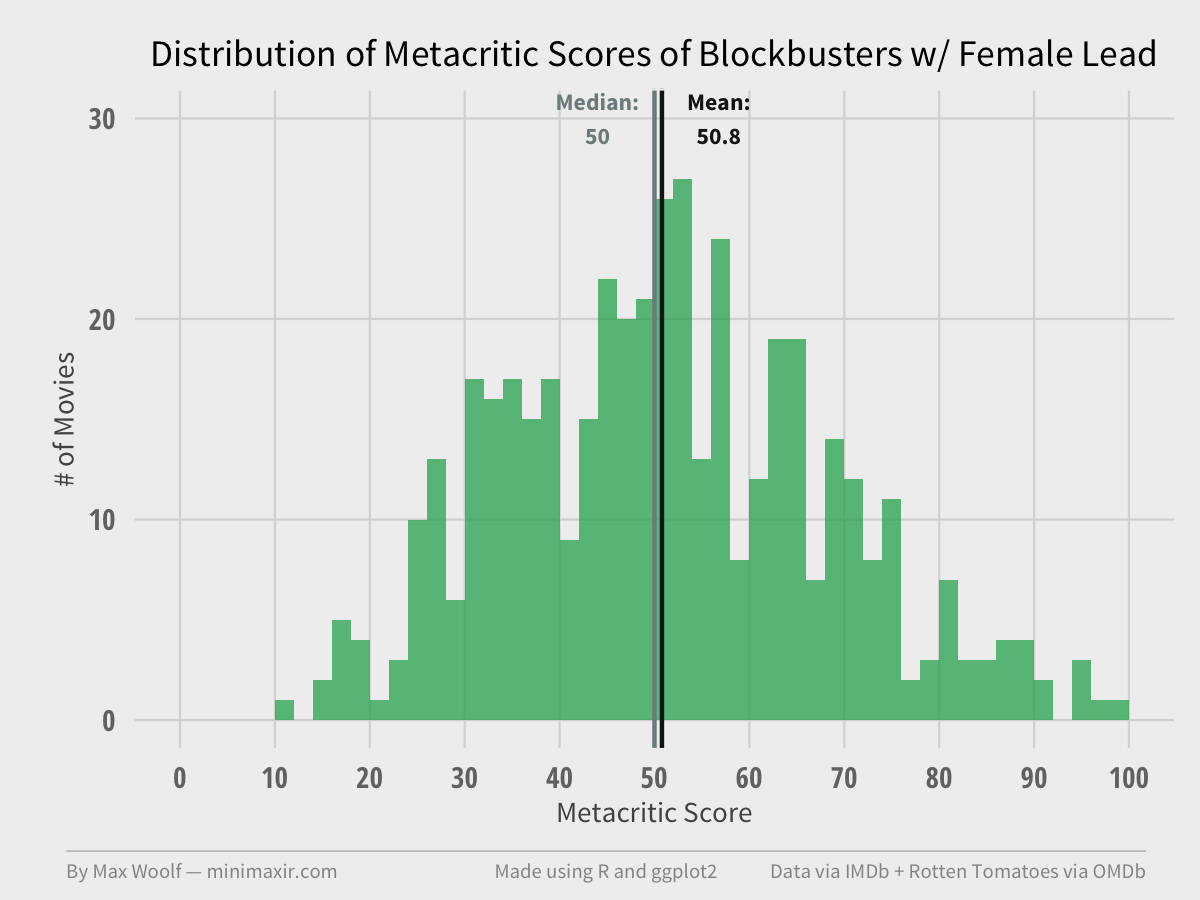
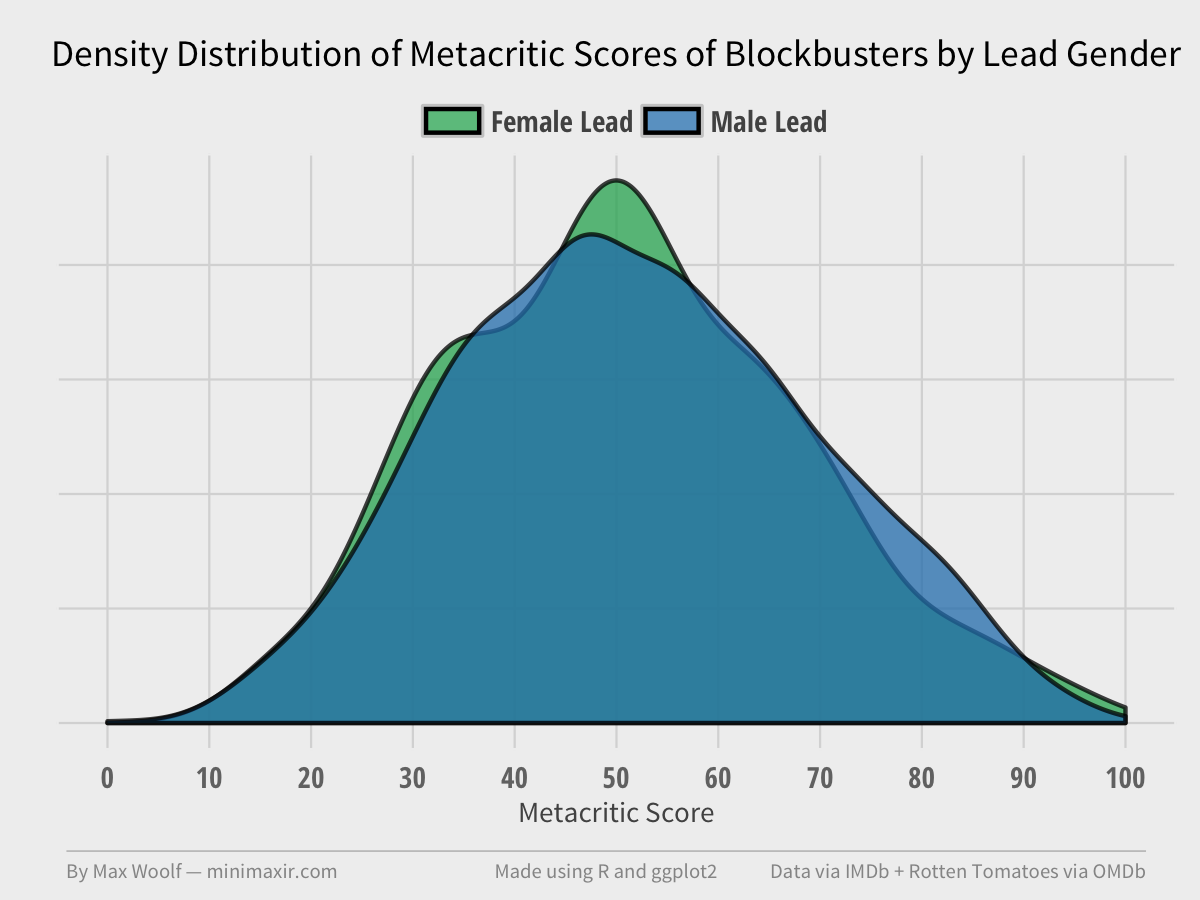
Again, distributions are the same (both take on the shape of a Normal distribution, interestingly). And again, the Kolmogorov–Smirnov test and the Wilcoxon rank-sum test fail. (p = 0.45 and p = 0.14 respectively).
The quality of a movie is independent from the gender of the lead actor in determining the financial performance of a movie.
Conclusion
In 2014, according to the MPAA, the gender breakdown of moviegoers who see blockbuster movies is about 50/50, eliminating another potential explanation for the average movie revenue discrepancy.
Granted, there still can be more work done, such as controlling on movie Genre in addition to gender. Is the gender of the lead actor a causal factor in a movie’s success? Not necessarily, and this analysis does not assert such. But there definitely is a revenue disparity that’s worth investigating, and it’s not just that “male-led movies are better.”
There may be more movies like Star Wars Episode VII where a movie with a female lead can hit almost a billion dollars domestically (e.g. Star Wars VIII). Things are looking upward, and it would not surprise me if the 22% revenue difference decreases and disappears in the next decade.
You can view the code used to process the data and generate the data visualizations in this Jupyter notebook, open-sourced on GitHub, or you can view as a PDF which is better if you are on a mobile device.
You are free to use the charts from this article however you wish, but it would be greatly appreciated if proper attribution is given to this article and/or myself!
